标题: 大家来打劫了! [打印本页]
作者:
天宫公主 时间: 2007-5-25 01:52 标题: 大家来打劫了!
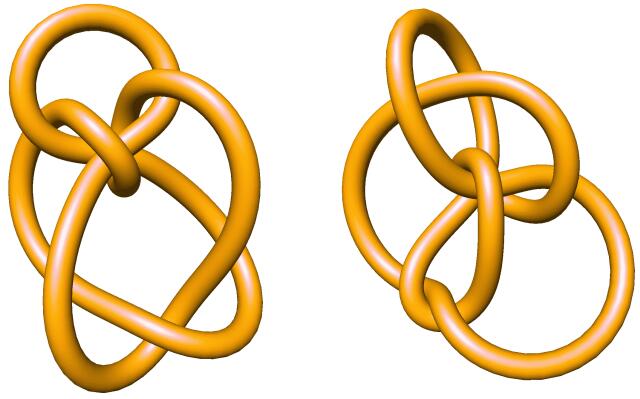
提问: 以上两个结是否相等?
P.S. 两个结相等, 当且仅当你可以在不剪开绳子的情况下, 把一个结转换成另外一个.
作者:
asky 时间: 2007-5-25 05:58
不等


作者:
grady0812 时间: 2007-5-25 07:36
不明白!
作者:
真宫望 时间: 2007-5-25 07:53
完全不是我擅长的类型....
作者:
水镜门生 时间: 2007-5-25 08:07
相等···不相等···相等就是不相等···不相等就是相等··
缠绵悱恻的中国结···
作者:
神灵风 时间: 2007-5-25 08:27
标题党
不相等,没模型转换不出来
作者:
TOP 时间: 2007-5-25 08:52
咳咳,topology玩玩什么不脱外套脱背心也就算了。knot theory未免有点……建议大家直接动手去试试看这两个东西究竟是结还是绳圈,大概要容易一点。
作者:
wang9990 时间: 2007-5-25 09:15
原帖由
TOP 于 2007-5-25 08:52 发表
咳咳,topology玩玩什么不脱外套脱背心也就算了。knot theory未免有点……建议大家直接动手去试试看这两个东西究竟是结还是绳圈,大概要容易一点。

本人最不在行的就是绕圈了。。。。。。。。。。LZ打中本人的弱点了。。。。。。。。。。
PS:哇,LS长得好象阿斗喔
作者:
真宫望 时间: 2007-5-25 10:40
楼上,你在公开场合笑话巡按使,准备接登闻鼓的罚单吧。
不过也可私了,200TB汇我帐上。我来打通关系。
最好有实物,这样光看看不出来。我要动手试。
作者:
ghostdance 时间: 2007-5-25 12:39
根据提问的逻辑,这两个结一定相等,且一定能够互相转换,具体怎么做,还是看到实际的形态才好摆弄,这样看没立体感,平面转化为三维思考能力不强的说,
作者:
天宫公主 时间: 2007-5-25 14:17
原帖由
TOP 于 2007-5-25 08:52 发表
咳咳,topology玩玩什么不脱外套脱背心也就算了。knot theory未免有点……建议大家直接动手去试试看这两个东西究竟是结还是绳圈,大概要容易一点。

这样好了,给个提示:这两个结相等。
想证明两个结不相等是个很难的事情,证明最简单的死结不能打开就废了人类大约2500年之久。但要是想证明两个结相等,自己拿根绳子做一个模型慢慢试好了。
作者:
太平清领道人 时间: 2007-5-25 17:26
好难哪。。。头晕,爬走。。。
作者:
墨叶 时间: 2007-5-25 17:33
除了试就没有其他方法吗??
作者:
风暴潮 时间: 2007-5-25 21:56
通过观察两个结是完全一样的,根本不用再转换。需要转换的就是观察角度,第二个在它的左侧看就跟第一个正面看一样
作者:
手冢国光 时间: 2007-5-25 22:01
晕,一点也不懂
作者:
墨叶 时间: 2007-5-25 22:09
原帖由 风暴潮 于 2007-5-25 21:56 发表
通过观察两个结是完全一样的,根本不用再转换。需要转换的就是观察角度,第二个在它的左侧看就跟第一个正面看一样
同意.
等公主回答.
作者:
墨叶 时间: 2007-5-25 22:18
再认真看下,又不对了.
中间结的有一点不同.
作者:
wayniudng 时间: 2007-5-25 23:33
经过测试```
∵A图≠B图
∴B图≠A图
=>
两图不等

作者:
青石 时间: 2007-5-26 01:39
有兴趣可以看看这个网页
http://katlas.math.toronto.edu/wiki/Main_Page
判断两个结不同到有不少方法
要判断是一样的 真的很难
或许 实物试验可能是最好的方法
北大的王诗宬院士在讲扭结时 经常拿根皮带示范
作者:
天宫公主 时间: 2007-5-26 01:46
青石,我不得不汗一下。你给那个链对解答这个问题毫无帮助啊!
作者:
颖颖 时间: 2007-5-26 01:47
公主,我不得不汗一个。本来青石那个链是没用的,可经过你这么一说它就有用了!
作者:
天宫公主 时间: 2007-5-26 01:48
颖颖你个小屁孩,胡说什么?你已经把答案告诉大家了。
好了,我提示完了。
作者:
青石 时间: 2007-5-26 01:49
原帖由 天宫公主 于 2007-5-26 01:46 发表
青石,我不得不汗一下。你给那个链对解答这个问题毫无帮助啊!
没说有用处阿
谁对扭结有兴趣可以去看看嘛
其实我的拓扑学的很糟糕
对扭结只知道一点点
作者:
TOP 时间: 2007-5-26 02:05
公主的提示已经很明显了,咳咳。至少是排除了相当部分的方案。大家可以少花不少时间。不过我是一向光说不练的,大家
作者:
nonsensor 时间: 2007-5-30 07:00
请问怎么建立模型?
作者:
天宫公主 时间: 2007-5-30 08:18
自己拿根绳子好了,然后可以用 webcam 照几张图片上来。或者用 Reidemeister moves 解释也可以,不过就不要求了。
作者:
幻火 时间: 2007-5-30 17:13
图片中左右两图不相同,左边是一根绳子的结,右边需要两根绳才能完成,这个有点类似基础的彼诺乌斯圈(好像是这个名字吧)
所以按照这个理论,只有把左边的结按照绳子的中心线剪开就成为右边的结了
纯理论分析,懒得动手懒得证明,错了就忽略吧
作者:
天宫公主 时间: 2007-6-1 15:06
这个。。。貌似这个观测是不对的。两个结都可以用一条绳子完成。
作者:
刀剑笑 时间: 2007-6-1 21:35
怎么看都象是两个死结....怎么能是相等的结呢?
作者:
秋旭 时间: 2007-6-2 13:11
相等,因为都是一条绳子打的,只要解开了都一样。
作者:
树-- 时间: 2007-6-20 10:32
两个结从图像上看起来相等,
第一个可以这么看,有一个8字结,中间交叉部分又有一根绳绕过而且与8字结下半部分交叉。
第二个其实分解看特征和第一个一样,不过角度转了大约90度,稍变型一下。
作者:
hh001 时间: 2007-6-21 11:09
乍一看,两图大体相似,只有中间的小结绕法有所不同。但也只有此处不同。
根据负负得正的原理,我认为两个结是不同。因为只有一处不同,实难转换!
作者:
风暴潮 时间: 2007-7-6 20:17
中间结附近的那几条绳子的上下中关系不是唯一的,可以有不同的理解方式。按照一般方式看理解绳子的上下关系的话两个结是一样的,只需要换个角度看。是不是绳子的上下中关系对结的相同与否没有关系,不论绳子怎么上下都是一样的结。
作者:
edyswghe 时间: 2007-7-20 18:09
相等的,右边那个图右下的圈转到上方,把三个圈的结合部分拉紧
作者:
霸王高宠 时间: 2007-8-5 18:23
相等,第二个结逆时针旋转90左右后倒置,ok(此题为2004年数学奥赛初赛题)
作者:
lypplay 时间: 2007-8-5 18:37
我看了5分钟,最后认为是一样的.

作者:
huyou75 时间: 2007-8-6 19:24
一样,只要注意看一下就会发现2是1翻转而成的
作者:
老一 时间: 2007-8-8 18:26
针对什么说的??理解不一样啊或许
| 欢迎光临 轩辕春秋文化论坛 (http://www.xycq.org.cn/forum/) |
Powered by Discuz! 5.0.0 |